
 |
www.WirelessCommunication.NLChapter: Wireless Propagation Channels
|
Transformed into constraints in the frequency domain, this criterion is found to be satisfied if the transmission bandwidth does not substantially exceed the 'coherence' bandwidth B_c of the channel. This is the bandwidth over which the channel transfer function remains virtually constant.
Formally the coherence bandwidth is the bandwidth for which the auto co-variance of the signal amplitudes at two extreme frequencies reduces from 1 to 0.5.
For a Rayleigh-fading channel
with an exponential delay profile, one
finds
B_c = 1/(2 pi T_rms)where T_rms is the rms delay spread.
Correlation of Fading
From the delay profile, one can compute the correlation of the fading
at different carrier frequencies.
The inverse transform of the delay profile gives the autocorrelation of the in-phase component I of a sinusoidal signal at frequency f_1 and f_2.
Delay Profile <- -> E [I(f_1) I(f_2) ]For reasons of symmetry, this is equal to the autocorrelation of the quadrature component. After some algebraic operations (elaborated in the slide show), this can be used to express the auto-correlation and auto-covariance of the amplitude, versus frequency separation f_1 - f_2.
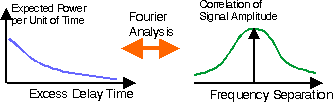
Figure Auto-Covariance of the received amplitude of
two carriers transmitted with certain frequency offset.
The normalized co-variance of the amplitudes R_1 and R_2 of two carriers, one at f_1 and another at f_2 is
E R_1 R_2 - E R_1 E R_2
C = ---------------------------
sigma(R_1) sigma(R_2)
That is, we normalized for unity standard deviations sigma of R_1 and R_2.
One finds, for an exponential delay profile
1
C = --------------------------------
1 + 4 pi^2 (f_1 - f_2)^2 T_rms^2