

|
JPL's Wireless Communication Reference WebsiteChapter: Analog and Digital Transmission, Receiver Design |
Contributed by Olivier Swedor, EPFL
A model of digital communication system:
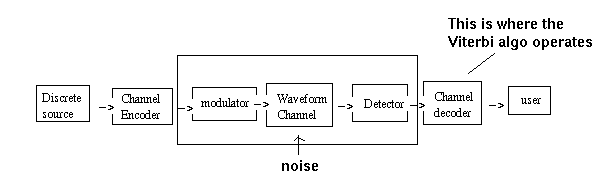
The discrete source generates information in the form of binary symbols. The
channel encoder adds redundancy to it according to a prescribed rule. The channel
decoder in the receiver uses this redundancy to decide wich message bits were
actually transmitted. The combined goal of the encoder and decoder is to minimize
the effect of channel noise.
There are many different error-correcting codes. They have been classified into
"block codes", or "convolutional codes", depending on wether there is a memory
in the encoder or not.
In block coding, an encoder generates a n - bit code word with a k - bit message block, so code words are produced on a block-by-block basis. But if we want to process the incoming bits serially rather than in large blocks, we will use convolutional coding.
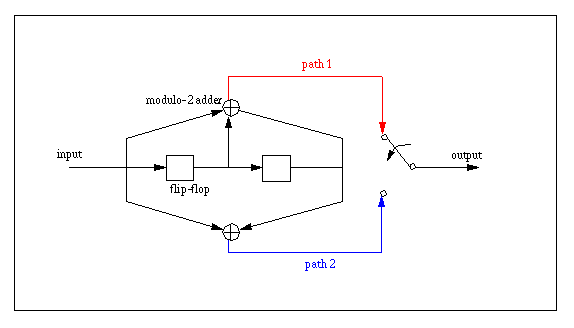
In convolutional codes, the encoding operation may be viewed as the discrete-time
convolution of the input sequence with the impulse response (or generator polynomial)
of the encoder. The encoder operates on the message with a "sliding window",
with a length equal to its own memory.
An example of convolutional encoding:
Source: Applet by Olivier Swedor. The development of this page has been carried out as a semester project in the mobile communications laboratory of the Swiss Federal Institute of Technology, EPFL, Lausanne.