

|
Wireless CommunicationChapter: Analog and Digital
Transmission
|
As is seen from the BER expression and (36), the MMSE cancellation of the MUI leads to a noise penalty. Two terms occur in the denominator, one is due to imperfect cancellation of MUI, the other is due to noise. The ICI is not actively cancelled, so its behaviour is similar to the noise. Figure 4, plots z and also the individual effects from MUI and noise, relative to the SNR per subcarrier. That is, it plots (M11/ (M22-M112)) / (PTTs/N0 ) and (M11Ts/ M02N0) / (PTTs/N0 ). It is seen that the noise penalty increases monotonically with the local-mean SNR.
Figure 4: MC-CDMA figure of merit z in dB versus the local-mean SNR on Rayleigh channel. MATLAB
Figure 5 plots the local-mean BER for BPSK versus the signal-to-noise ratio (SNR) in a very-slowly changing Rayleigh-fading channel, without Doppler spread and ICI (v = 0). Curves (AWGN), (OFDM) and (3 - MC-CDMA) are theoretical results. Curve (AWGN) depicts the BER of BPSK in a channel without fading, using erfcÖ (EN/N0). Curve (OFDM) gives the BER for a narrowband Rayleigh fading channel (N = 1) which is the same as the local-mean BER for OFDM, before any error correction. Moreover, it models MC-CDMA with N = 1. Curve (3) is the local-mean BER for MC-CDMA for N ® ¥ . Curve (1) and (2) are Monte Carlo simulations for a system with N is 8 and 64 subcarriers, respectively.
Curves (4) and (5) for correlated Rayleigh fading have been simulated in the frequency domain. All subcarrier amplitudes are known to be zero-mean complex Gaussian with covariance matrix G [17-26
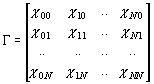 (37)
(37)
with
![]() , (38)
, (38)
where TRMS is the delay spread of the radio channel. In a Monte-Carlo simulation we generated channels from an i.i.d vector of complex Gaussian random variables G, with unity variance and length N. This vector was then multiplied by an N-by-N matrix A, such that AAH = G , to create diag(H) = [b 0,0 b 1,1 , .. ,b n,n ] = A G, and b m,n = 0 for n ¹ m (no Doppler). Then, the weight vector diag(W) was determined from diag(H). This results in amplitudes for the wanted signal (x0), amplitudes for the MUI and a noise amplification term. So the BER for this particular channel can be calculated. Average BER's have been obtained by repeating this process for different channels G.
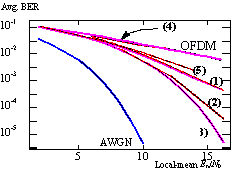
Figure 5: Local-mean average BER versus Signal-to-Noise ratio. Theory: (3, AWGN, OFDM) and simulations (1, 2, 4, 5). ("AWGN"): BPSK, no-fading, AWGN ("OFDM"): (1): N = 8, uncorrelated fading, (2): N = 8, highly correlated fading, (3): Infinitely many subcarriers, (4) N = 8, highly correlated fading, (4) N = 8, lightly correlated fading
The average BER versus the SNR for correlated fading was also simulated for
the case of N = 8with TRMS/Ts.= 0.001 and 0.125, in curve (4) and (5), respectively. Results show that the assumption of I.I.D. fading at the subcarriers is optimistic.
The differences amoung the curves (3) and those for finite N are due to the fact that the SNR after despreading still contains fading. The slope of the curve for large SNR is determined mainly by the 'resolvable' number of independently fading channel components, which is approximately equal to min(N, TRMS/Ts.+1).
MATLAB
JavaScript
The effect of Doppler spreading at 4 GHz is introduced in Figure 7. Here we consider a system with (infinitely) many subcarriers. We inserted typical values for DTTB but modified it to MC-CDMA instead of the standardized OFDM. The frame duration is 896 microseconds, with an FFT size of 8192. This corresponds to a subcarrier spacing of fs = 1.17 kHz and a data rate of 9.14 Msymbols/s. Figure 7 shows the local-mean BER versus antenna speeds v for Eb/N0 of 10, 20 and 30 dB. While MC-CDMA appears to largely outperform uncoded OFDM.