Wireless Communication Chapter: Analog and Digital Transmission Section: Multi-Carrier Modulation, OFDM, Effect of Doppler

Discrete-Frequency Channel Model for OFDM

This page develops a model for a channel representation starting from the classic multipath description, using a collection of I_w reflected waves. Each wave has its particular Doppler frequency offset w _i, path delay T_i and amplitude D_i. The frequency offset lies within the Doppler spread -2p f_D < w _i < 2p f_D , with f_D = v_s f_c/c. Here v_s is the velocity of the mobile antenna, c is the speed of light and the carrier frequency is w _c = 2p f_c. More precisely, the Doppler shift of the i-th wave is w _i = (2p v_s/c) f_c cos(q _i) with q _i the angle of arrival. Let f_s denote the spacing between the adjacent subcarriers and w _s = 2p f_s. The received signal equals

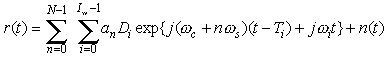
here n(t) is additive white Gaussian noise. We will denote the vector of modulation symbols as A = [a₀, a₁, ...a_N-1]^T. The transmit energy per subcarrier is E_N = E |a_n|². Not all reflected waves are individually ‘resolvable’, that is, a receiver sampling in a time-window of finite duration will only see the collective effect of multiple reflected waves within a certain time-frequency window.

The narrowband mobile channel model can be compacted into a complex received amplitude that is time varying. We rewrite the received signal as

where the time-varying channel amplitude V_n(t) at the n-th subcarrier is

A Tayler expansion is V_n(t) = v_n⁽⁰⁾ (t₀)+ v_n⁽¹⁾ (t₀) (t - t₀) + v_n⁽²⁾ (t₀) (t -t₀)² / 2 + .. .

See an animation of a Rayleigh fading complex amplitude. Have the amplitude plotted for you live on screen, and imagine what values the derivatives take on.

Here v_n^(q) (t₀) denotes the q-th derivative of the amplitude with respect to time, at instant t = t₀. If the Doppler spread is much smaller than the frequency resolution of the FFT grid, we may restrict our analysis to zero and first order effects. In a Rayleigh channel, v_n^(q) is zero-mean complex Gaussian for any n and q. To characterize the channel, we are interested in the covariance of variables v_n^(p) and v_m^(q), viz., Ev_n^(p)v_m*^(q), where * denotes the complex conjugate. In [20], we have derived this for an exponential delay spread and a uniform angle of arrival. The covariance becomes, for p + q even, (3)

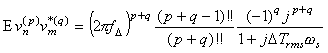
and Ev_n^(p)v_m*^(q) = 0 for p + q is odd.

Discrete-Frequency Link Model

In OFDM, a frame of N symbols is detected by taking N samples and performing an FFT. In other words, detection of the signal at subcarrier m occurs by correlation with a complex sinusoid having the frequency of the m-th subcarrier, viz., exp{-jw _ct-j(m-D _f)w _st } during the symbol duration NT. Here D_f is the frequency offset normalized to the subcarrier spacing w _s. In the sampling process, the receiver makes a timing error _t, where D _t is the time offset normalized to a sample interval T = (N f_s)- ¹. That is, it samples at t = D_t, D_t + T, D_t + 2T, ... . We assume that cyclic prefixes avoid any interframe interference. We use Y as the vector of length N to denote the output of the FFT in the receiver. The m-th output of the FFT is found as

Here, m = 0, 1, ..., N - 1 and Y = [y₀ , y₁, ... , y_N-1]^T. We observe that w _sT = 2p/N. We introduce the OFDM system parameter x_D^(q), defined as

to describe the signal transfer over the q-th derivative of the amplitude at subcarier n to the (n+D )-th receive subcarrier. This allows us to rewrite y_m as follows:

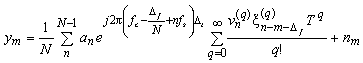
In particular, we will consider the first two terms of the expansion, and we denote c_D = x_D⁽⁰⁾ and z_D = x_D⁽¹⁾. So,

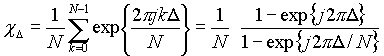
For integer D , cD reduces to d_D , which is just a confirmation that subcarriers (with a nonfading amplitude) are orthogonal. Note further that

for integer and non-zero D , we see that

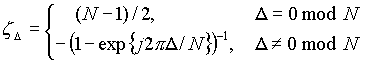
Roughly speaking z_D / z₀ » (jp D )^-1, with D = 1, 2, 3, ...., so the ICI reduces slowly with increasing subcarrier separation. Relatively many subcarriers make a significant contribution to the ICI. We define vector V = [v₀, v₁, .., v_N-1] for the subcarrier amplitudes and V’ = [v₀⁽¹⁾, v₁⁽¹⁾, .., v_N-1⁽¹⁾]^T for the derivatives.

For an ideally synchronizing receiver, i.e., with D_t = 0 and D_f = 0,, the received signal Y can compactly be written in Discrete Frequency domain as,

with DIAG(X) the diagonal matrix composed of the elements of vector X, and

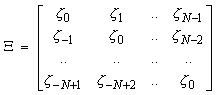
Not all terms in X address ICI: In the expression, the diagonal terms z₀ carry signal components from the n subcarrier to the n-th subcarrier, so in fact the receiver sees a signal amplitude of (c₀ v_n + ^z₀ T v_n⁽¹⁾)a_n. To address this in the following calculations we define X^* = X - z₀ I_N. The wanted signal component in a conventional receiver equals V+z₀ V’T, which in practice closely approximates V, except in deep fades.

Figure 1 depicts the channel and receiver in the discrete frequency domain. Thus, the FFT is not drawn explicitly. In a conventional system, W represents the equalizer, or automatic gain control per subcarrier, to compensate for fading on the subcarriers.

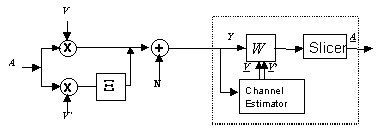
Figure 1: Discrete-Frequency representation for the Doppler multipath channel and a (feedforward) OFDM receiver

Next: how to build a receiver based on this principle?

Wireless Communication © Jean-Paul M.G. Linnartz, 2001.

Publications for scientific reference:

The key ideas of this page have been published first in: J.P.M.G. Linnartz and A. Gorokhov, "New Equalization approach for OFDM over dispersive and rapidly time varying channel", PIMRC 2000, London.

Journal Publication:

450k PDF A. Gorokhov, J.P.M.G. Linnartz, "Robust OFDM receivers for dispersive time varying channels: equalization and channel acquisition", IEEE Transactions on Communications, Vol. 52, No. 4, april 2004, pp. 572-583

PDF 500k S. Tomasin, A. Gorokhov H. Yang, J.P.M.G. Linnartz, "Iterative Interference cancellation and channel estimation for mobile OFDM", IEEE Transaction in Wireless Communication, Vol. 4, No. 1, Jan. 2005, pp. 238-245.