Probability of Successful Transmission

ALOHA (orange), 1-persistent CSMA (green), non-persistent CSMA (blue)
d : Carrier Sensing Delay, relative to packet time
Offered Traffic: average of 1 packet per slot time
Mobile slowly Rayleigh-fading channel
Plane-earth path loss: attenuation = 40 log (distance)
Uniform distribution of terminals in circular area
Capture threshold z = 4 (6 dB C/I ratio needed)

Note:

For non-persistent CSMA, some attempts do not lead to transmission. So, P(success) is not unity for a terminal near base station.

Packet Success Probability in Slotted ALOHA

Fundamental property of independent (Poisson) arrivals:

Probability of n packets interfering with test packet (total n+1 packets)

Poisson probability P_n(n) of n contending signals in same slot is

The probability Q(r) of a successful transmission is

Throughput of Slotted ALOHA

The total packet throughput is

where

q_n

C_i

Special case: no capture

q_n(r) = q_n

q₀

All effects of terminal location vanish.

The probability Q(r) of a successful transmission is

Q(r)

p_n

G_t

The total packet throughput is

S_t

G_t

p_n

G_t

Another way to arrive at this result is

S_t

p_n

G_t

Both methods give the classical expression S_t = G_t exp(- G_t)

INHIBIT SENSE MULTIPLE ACCESS

Outbound signalling channel:

receiver status: busy or idle.
acknowledgements

Time-Space diagram for ISMA
with busy and idle period

Busy Period

A Busy period contains

an inhibited period,
a period in which the base station sends busy signal,
plus
a vulnerable period,
a period in which a packet has arrived at the base station but no busy tone is received yet.
Duration of vulnerable period: signalling delay d.

Calculation of Length of busy period

Basic assumption: same delay d for all terminals

Add:

+ one packet time (unity duration)
+ busy-tone turn-off delay (d)

+ additional duration y because of colliding packets arrive with time offset, where

y = d₁- length of period with no arrivals

The busy period has average duration

Idle period

•Idle period is the time interval from end of busy tone till arrival of new packet
•For Poisson arrivals and no propagation delays:

· Memoryless property of Poisson arrivals:

· Expected duration I of idle period

= the average time until a new packet arrival occurs,

•Thus, E I = G_t^-1

Cycle

one cycle = idle period + busy period

Renewal Reward Theorem

Throughput per unit of time =

Expected throughput per cycle
_________________________
Expected length per cycle

Non-p. ISMA without Delay without Capture

If a packet arrives when the base station transmits a "busy" signal

•The attempt fails.
•The packet is rescheduled for later transmission.

•It contributes to G, but not to S

•Retransmissions also contribute to G

If a packet arrives in the idle period

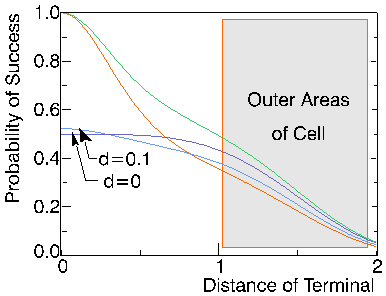
•The transmission is successful
·No interference can occur (d = 0)
·Channel is assumed perfect

•This occurs with probability EI/(EI + EB)

Using the renewal reward theorem, the throughput becomes

Non-persistent ISMA in Mobile Channel

Probability of successful transmission Q(r)

•Take account of the three possible events
·Arrival in idle period
·Arrival in vulnerable period

·Arrival in busy period

If a packet arrives when the base station transmits a "busy" signal

•The attempt fails.

If a packet arrives in the idle period

•This occurs with probability EI/(EI + EB)
•We call this packet an "initiating packet"

•A collision occurs if other terminals start transmitting during delay d of the inhibit signal.

•Probability of n interfering transmissions is Poissonian, with

Non-persistent ISMA: Probability of success

If a packet arrives in the vulnerable period

•Channel is "busy" but seems "idle
•It occurs with probability d/(EB + EI).

•Packet is NOT inhibited

•It always interferers with the initiating packet

•This packet experiences interference from at least one other packet

•Additional n - 1 contending signals are Poisson distributed. Conditional probability of n interferers is

with n = 1, 2, ... .

Total Throughput of non-persistent ISMA

Use the following results:

•Average cycle length EI + EB
•Initiating packet plus Poisson arrivals during period d

Special case : instantaneous inhibit signalling (d® 0)

•collisions can never occur in non-persistent ISMA.
•S_t ®G_t(1 + G_t)^-1.

•S_t ®1 for G_t ® ¥.

1-Persistent unslotted ISMA

•Waiting terminal may start transmitting as soon as previous transmission is terminated
•Busy period can consist of a number of packet transmissions in succession

• We consider no signalling delay (d = 0).

•For large offered traffic (G® ¥ ), throughput rapidly decreases (with exp{-G})

Transmission cycle in 1-p ISMA

Throughput of 1-Persistent unslotted ISMA

Cycle-initiating packet

•If a packet arrives during idle period
•Probability of correct reception is q₀(r).

During transmission of (initiating) packet

•A random number of k terminals sense the channel busy
•k is Poissonian with probability P_n(k).

•When the channel goes idle, k terminals start transmitting

Probability that busy period terminates

•Probability that no terminals starts transmitting, (k = 0) is exp (-G_t)
•Probability P_m(m) of transmissions during m units of time, concatenated to initiating packet is

•Average duration of busy period

Probability of a successful transmission Q(r)

Successful packet arrive in idle or vulnerble period

Capture probability:

Inserting EB and EI=G_t^-1and capture probabilities gives

Throughput of 1-Persistent unslotted ISMA

Total channel throughput S_t

where

C₁ is probability of success if no interference is present
C_i is probability of success when i packets collide

Special case

•1-persistent CSMA on wired channels
(q₀=1 and q_n=0 for n = 1, 2, ...)