www.WirelessCommunication.NL

Poisson Arrival Process

A commonly used model for random, mutually independent message arrivals is the Poisson process. The Poisson distribution can be obtained by evaluating the following assumptions for arrivals during an infinitesimal short period of time delta t

The probability that one arrival occurs between t and t+delta t is t + o( t), where is a constant, independent of the time t, and independent of arrivals in earlier intervals. is called the arrival rate.
The number of arrivals in non-overlapping intervals are statistically independent.
The probability of two or more arrivals happening during t is negligible compared to the probability of zero or one arrival, i.e., it is of the order o( t).

Combining the first and third assumption, the probability of no arrivals during the interval t, t+ delta t is found to be 1-

t + o( t).

Arrival Rate

The arrival rate

is expressed in the average number of arrivals during a unit of time.

Some Interesting Properties

The probability P_n of n packet arrivals in a time interval T becomes

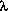      (T)^n
P_n  =  -----  exp{-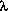T}
         n!

The distribution of the number of arrivals in a time interval of t,t+T is independent of starting time t.
The probability of n other arrivals, in addition to a given "test" arrival that is known to be present is exactly the same as the probability of n arrivals without any a priori assumptions. The test arrival has no influence on other arrivals. This property is used, for instance, in the calculation of the throughput of random-access schemes, such as slotted ALOHA, in radio networks with capture.
The probability of no arrivals during period of duration T is
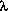```
f(T)  = exp{- T}
```
where f ( ) is the probability density function of the duration between two arrivals. Thus, interarrival times have a negative exponential distribution with mean 1/.

Applications

The Poisson process is used to model

the arrival of new telephone calls
message arrivals in packet-data network

www.WirelessCommunication.NL

Poisson Arrival Process

Arrival Rate

Some Interesting Properties

Applications

www.WirelessCommunication.NL © 1993, 1995, 1999.